23:最小的k个数
题目描述
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
简单题。。。。
function GetLeastNumbers_Solution(input, k){ if(k>input.length) return []; let ans = []; input = input.sort(); //console.log(input.join("").slice(0,4).split("")); input.join("").slice(0,k).split("").map(function(item,index) { ans.push(parseInt(item)) }); return ans; } 24:连续子数组的最大和
题目描述
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。你会不会被他忽悠住?(子向量的长度至少是1)
dp入门题,几年前做了这么一道(加上记录位置的):
function FindGreatestSumOfSubArray(array){ let len = array.length; let max = -Infinity; let tmp = 0; let sum = 0; for(let i = 0; i < len; i++) { sum+=array[i]; if(sum>max) { max = sum; } if(sum<0) { sum = 0; } } return max;} 25:链表中环的入口节点
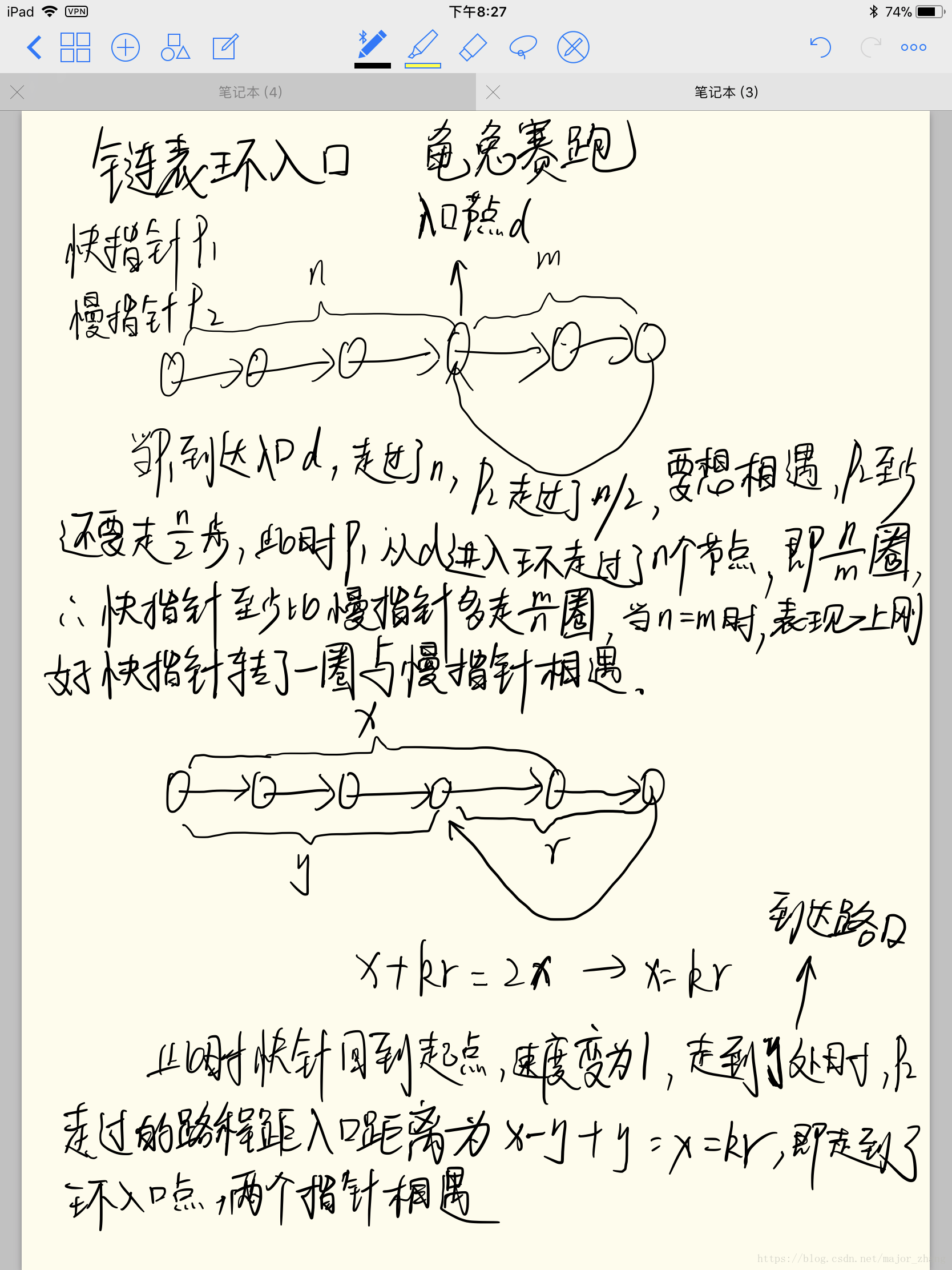
龟兔赛跑法:
第一步,找环中相汇点。分别用p1,p2指向链表头部,p1每次走一步,p2每次走二步,直到p1==p2找到在环中的相汇点。
第二步,找环的入口。接上步,当p1==p2时,p2所经过节点数为2x,p1所经过节点数为x,设环中有n个节点,p2比p1多走k圈有2x=kn+x; kn=x;可以看出p1实际走了k个环的步数,再让p2指向链表头部,p1位置不变,p1,p2每次走一步直到p1==p2; 此时p1指向环的入口。证明:
注意,一定要控制好边界!否则oj还是报访问错误的错,通过率0!
/*function ListNode(x){ this.val = x; this.next = null;}*/function EntryNodeOfLoop(pHead){ //只有1个节点或者0个节点直接返回null,因为这样不可能产生环 if(pHead == null || pHead.next == null) return null; let p1 = pHead; let p2 = pHead; //很巧妙,null是没有next的,否则oj会报访问越界错误,判断p2可走再p2.next可否走即可 while(p2 !==null && p2.next !== null) { p1 = p1.next; p2 = p2.next.next; if(p1 === p2) { p1 = pHead; while(p1!==p2) { p1 = p1.next; p2 = p2.next; } if(p1 === p2) return p1; } } return null;}